COMP557程序代写、代做c++,Python程序
COMP331/COMP557 Optimisation
Programming Assignment
Due date: Thursday, December 10th, 2020, noon, via SAM
This assignment is worth 10% of your grade.
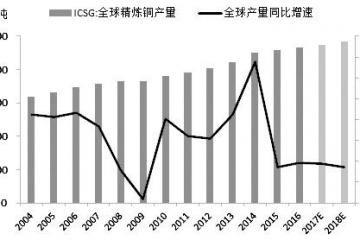
We are given a triangular array of 36 nodes in the plane that are connected among each other as follows.
A small triangle is a set of three adjacent nodes. If two small triangles share two nodes, then they form a small
rhombus. In each small rhombus, two nodes are at obtuse corners and two nodes are at acute corners:
Each of the 36 nodes gets assigned a height, which is a real number. Hence,
by linear interpolation between the nodes, a height vector h ∈ R
36 gives rise
to a triangulation of a surface in 3-dimensional space that on a small rhombus
looks as the picture on the right.
We will only consider those height vectors that have fixed heights as follows on the nodes at the boundary:
A height vector h ∈ R
36 is called mountain if for all small rhombi (in all three rotations) we have that the sum
of the heights of the nodes at the obtuse corners is at least as high as the sum of the nodes at the acute corners.
1/2
COMP331/COMP557 Optimisation
Here is an example of a mountain:
The inequalities for all small rhombi are satisfied, for example 6+4 ≥ 10+0 and 10+4 ≥ 6+7 and 10+6 ≥ 12+4.
A weighting w ∈ R
36 is a vector of real numbers. For a given weighting w, the w-weight weightw(h) of a
mountain h is defined as
weightw(h) = X
node v
w(v) · h(v).
For a given weighting w, a mountain h is called w-optimal if there is no other mountain with a higher w-weight.
The set of mountains whose heights at the boundary nodes are as illustrated in Figure 1 forms a polytope
in R
15. Your taks is to experimentally determine the number of the polytope’s vertices. This shall be done by
choosing random linear objective functions and maximising them within the polytope.
1. Write a function (in any programming language) that picks a random weighting w and writes to the disk
an .lp file whose optimal solution is a w-optimal mountain.
2. Write a program that calls the above function 1000 times to generate 1000 .lp files, calls glpsol on those
files and analyses the output. After this analysis, the program should output the set of distinct mountains
that were found.
3. For each mountain that was found, draw a picture analogous to Figure 2. Put them in a single .pdf file.
Submission format: Put the following into a single .zip file:
1. The program code.
2. The 1000 .lp files.
3. The .pdf file containing the figures of the mountains analogous to Figure 2.
2/2
如有需要,请加QQ:99515681 或邮箱:99515681@qq.com 微信:codehelp
郑重声明:此文内容为本网站转载企业宣传资讯,目的在于传播更多信息,与本站立场无关。仅供读者参考,并请自行核实相关内容。